对Neural Networks and Deep Learning 的理解

可能是我自己对于机器学习的基础掌握的不是很好，在我阅读这篇文章的时候对好多地方都有困惑。

1. 比如文中提到了Sigmoid函数，为什么会有这个函数，换做别的函数可不可以呢？
2. 梯度下降是由什么数学背景运算得到的，梯度下降个的向量化是个什么意思

显然作者在写文章的时候虽然是面向初学者介绍机器学习的内容，但是在具体到内容的时候还是给我这样的初学者挖了很多坑。这篇文章主要是介绍我自己对文章的理解和一些笔记。

基本原理

机器学习算法的实现一共三步。听起来很简单，但是其中的数学知识一旦不够还是很难理解的。

1. 寻找合适预测函数。在神经网络那篇文章里，作者只是在开篇介绍了一下感知机和Sigmoid函数，并没有说明在实际编程的时候用什么函数。其实这步是非常关键的，因为他会确定我们到底是应该使用线性函数还是非线性函数。其实这个时候就是Sigmoid函数发挥作用了。
2. 构造一个损失函数（Cost），用来表示预测输出和期待值之间的偏差。可以二者之间的差或者其他形式。最终将所有的Cost求和或者平均，得到最终的损失函数J
3. J最小时就可以得到最合适的预测函数，为了快速的计算J的最小值就引进了梯度下降算法（其实还有一种是梯度上升算法）

具体过程

1. 构造预测函数 刚才也说到了在神经网络和深度学习这本书中并没有具体介绍预测函数的实现过程，只是简单的说了一个Simgmoid函数,但是并没有解释缘由。  
   
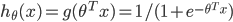
   这个函数有一个很好的特性是可以根据输入的值得到两种类型的结果，线性的和非线性的。
   构造函数：
    
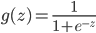
   hθ(x)函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：
   

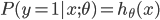
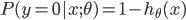
2. 构造损失函数
   构造函数是根据预测函数来计算的到的：
    
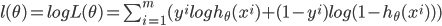
   构造函数就是在预测函数的基础上运用最大似然估计推导出最终形式：
    
   
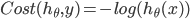
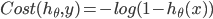
   具体的推到过程可以自己试一下。不是很复杂。

3. 梯度下降运算
   求解损失函数的最小值使用的就是梯度下降算法. 求J(θ)的最小值可以使用梯度下降法，根据梯度下降法可得θ的更新过程：  
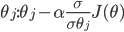     式中为α学习速率，学习速率也是一个需要设定好的值，他会决定机器学习的准备率和速度。 经过最终推导我们可以得到一下变化函数  
   

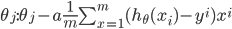
代码分析

下面就是原作者给出的完整机器识别代码，我们可以找到预测函数的原始模型
return sigmoid(z)*(1-sigmoid(z))
还有梯度下降的方法
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None)
在梯度下降算法中就包含了向量化的过程
` def update_mini_batch(self, mini_batch, eta):`

network.py
\~~~~~~~~~~

A module to implement the stochastic gradient descent learning
algorithm for a feedforward neural network.  Gradients are calculated
using backpropagation.  Note that I have focused on making the code
simple, easily readable, and easily modifiable.  It is not optimized,
and omits many desirable features.
"""

#### Libraries
# Standard library
import random

# Third-party libraries
import numpy as np

class Network(object):

def __init__(self, sizes):
    """The list ``sizes`` contains the number of neurons in the
    respective layers of the network.  For example, if the list
    was [2, 3, 1] then it would be a three-layer network, with the
    first layer containing 2 neurons, the second layer 3 neurons,
    and the third layer 1 neuron.  The biases and weights for the
    network are initialized randomly, using a Gaussian
    distribution with mean 0, and variance 1.  Note that the first
    layer is assumed to be an input layer, and by convention we
    won't set any biases for those neurons, since biases are only
    ever used in computing the outputs from later layers."""
    self.num_layers = len(sizes)
    self.sizes = sizes
    self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
    self.weights = [np.random.randn(y, x)
                    for x, y in zip(sizes[:-1], sizes[1:])]

def feedforward(self, a):
    """Return the output of the network if ``a`` is input."""
    for b, w in zip(self.biases, self.weights):
        a = sigmoid(np.dot(w, a)+b)
    return a

def SGD(self, training_data, epochs, mini_batch_size, eta,
        test_data=None):
    """Train the neural network using mini-batch stochastic
    gradient descent.  The ``training_data`` is a list of tuples
    ``(x, y)`` representing the training inputs and the desired
    outputs.  The other non-optional parameters are
    self-explanatory.  If ``test_data`` is provided then the
    network will be evaluated against the test data after each
    epoch, and partial progress printed out.  This is useful for
    tracking progress, but slows things down substantially."""
    if test_data: n_test = len(test_data)
    n = len(training_data)
    for j in xrange(epochs):
        random.shuffle(training_data)
        mini_batches = [
            training_data[k:k+mini_batch_size]
            for k in xrange(0, n, mini_batch_size)]
        for mini_batch in mini_batches:
            self.update_mini_batch(mini_batch, eta)
        if test_data:
            print "Epoch {0}: {1} / {2}".format(
                j, self.evaluate(test_data), n_test)
        else:
            print "Epoch {0} complete".format(j)

def update_mini_batch(self, mini_batch, eta):
    """Update the network's weights and biases by applying
    gradient descent using backpropagation to a single mini batch.
    The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
    is the learning rate."""
    nabla_b = [np.zeros(b.shape) for b in self.biases]
    nabla_w = [np.zeros(w.shape) for w in self.weights]
    for x, y in mini_batch:
        delta_nabla_b, delta_nabla_w = self.backprop(x, y)
        nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
        nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
    self.weights = [w-(eta/len(mini_batch))*nw
                    for w, nw in zip(self.weights, nabla_w)]
    self.biases = [b-(eta/len(mini_batch))*nb
                   for b, nb in zip(self.biases, nabla_b)]

def backprop(self, x, y):
    """Return a tuple ``(nabla_b, nabla_w)`` representing the
    gradient for the cost function C_x.  ``nabla_b`` and
    ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
    to ``self.biases`` and ``self.weights``."""
    nabla_b = [np.zeros(b.shape) for b in self.biases]
    nabla_w = [np.zeros(w.shape) for w in self.weights]
    # feedforward
    activation = x
    activations = [x] # list to store all the activations, layer by layer
    zs = [] # list to store all the z vectors, layer by layer
    for b, w in zip(self.biases, self.weights):
        z = np.dot(w, activation)+b
        zs.append(z)
        activation = sigmoid(z)
        activations.append(activation)
    # backward pass
    delta = self.cost_derivative(activations[-1], y) * \
        sigmoid_prime(zs[-1])
    nabla_b[-1] = delta
    nabla_w[-1] = np.dot(delta, activations[-2].transpose())
    # Note that the variable l in the loop below is used a little
    # differently to the notation in Chapter 2 of the book.  Here,
    # l = 1 means the last layer of neurons, l = 2 is the
    # second-last layer, and so on.  It's a renumbering of the
    # scheme in the book, used here to take advantage of the fact
    # that Python can use negative indices in lists.
    for l in xrange(2, self.num_layers):
        z = zs[-l]
        sp = sigmoid_prime(z)
        delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
        nabla_b[-l] = delta
        nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
    return (nabla_b, nabla_w)

def evaluate(self, test_data):
    """Return the number of test inputs for which the neural
    network outputs the correct result. Note that the neural
    network's output is assumed to be the index of whichever
    neuron in the final layer has the highest activation."""
    test_results = [(np.argmax(self.feedforward(x)), y)
                    for (x, y) in test_data]
    return sum(int(x == y) for (x, y) in test_results)

def cost_derivative(self, output_activations, y):
    """Return the vector of partial derivatives \partial C_x /
    \partial a for the output activations."""
    return (output_activations-y)

#### Miscellaneous functions
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))